Turbicône

[Turbi]

Re,

En extra voici un gif en couleur avec toute la gamme des paramètres p.

Yves

[pascal HA PHAM]

Bonjour,
belles animations et explications indispensables pour comprendre !
merci Yves....

dans un de tes post tu écrivais :

"On verra que d'autres transformations conduisent aussi à d'autres types de machines que les zz. "

pourra tu nous en dire plus sur ces autres types de machines ?

A+

Pascal

[Turbi]

Bonjour Pascal,

Il faut que je les finisse ces autres machines... Encore du travail...

En attendant, voici quelques autres GIF sur la géométrie du turbicône. Sur ces deux premières images, on voit comment prendre les symétriques de l'ellipse sphérique par rapport aux côtés du triangle sphérique équilatéral rectangle :

Puis en enlevant complètement les triangles, on obtient un système de huit ellipses sphériques qui roulent les une sur les autres. La transparence de la sphère sur la seconde image permet de voir ce qui se passe derrière :

Voilà pour le système de turbicônes.

À plus

Yves

[Cuicui]

voici quelques autres GIF sur la géométrie du turbicône.

Toujours aussi étonnant ! Merci Yves.

[Turbi]

Merci Cuicui,

C'est en bonne partie en habillant cette géométrie qu'on définit nos machines. Alors j'essaye avec les GIF de la rendre plus évidente. Après ça les explications sont normalement plus simples...

Voici donc une adaptation du modèle Turbicône pour les machines ZZ.
Dans un premier temps on définit une parallèle à l'ellipse sphérique complémentaire (en rouge). Ce qui permet ensuite de placer trois petits cercles centrés aux sommets du triangle sphérique, qui restent tangents à cette parallèle. C'est évidemment une bonne manière d'arrondir les angles.

Attention, même si elle semble en être une, la courbe parallèle n'est pas une ellipse sphérique.
Voici enfin le modèle utilisé dans les machines ZZ.


À bientôt

Yves

[Turbi]

Re Cuicui,

En fait tous ces GIF sont aussi pour moi la recherche d'un moyen d'exprimer la géométrie sur le WEB. Le gros avantage qu'ils ont c'est qu'il n'y a rien à faire pour déclencher les animations qu'ils contiennent. Elles démarrent toutes seules. Ca me semble donc un bon outil.

Merci de cet intérêt pour nos travaux.

À plus

Yves

[Turbi]

Bonjour,

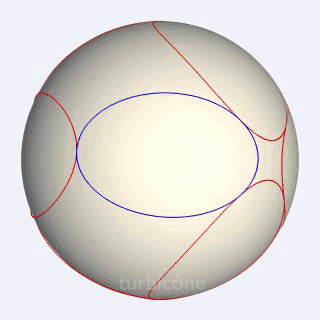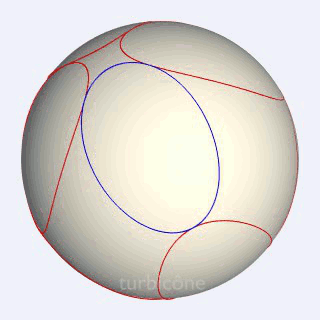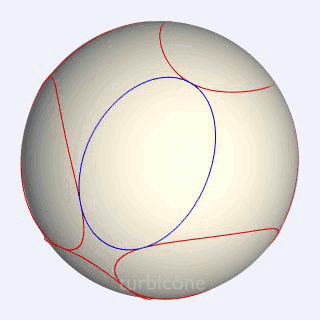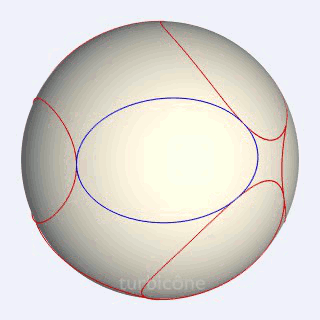
Un petit mot cette fois sur l'«extrusion conique». C'est l'opération utilisée pour passer des courbes sphériques aux pièces solides. En fait, l'opération consiste à générer à partir du centre de la sphère, les cônes qui passent par ces courbes, et à n'en retenir que la partie située entre la sphère initiale et une autre sphère ayant le même centre.

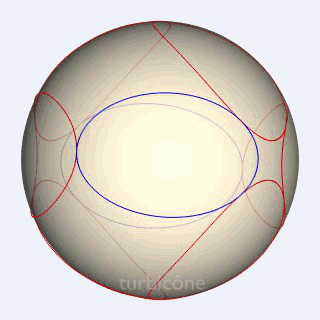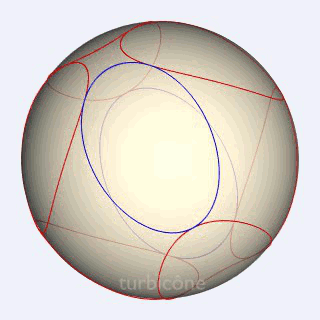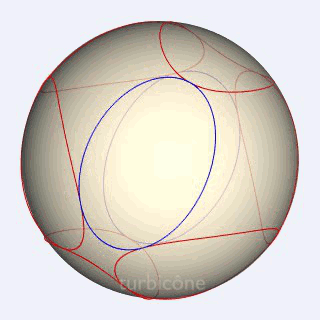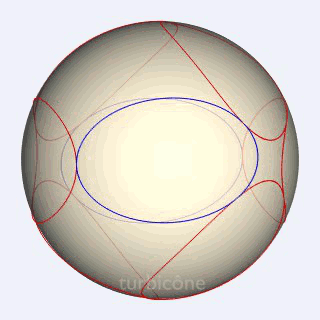
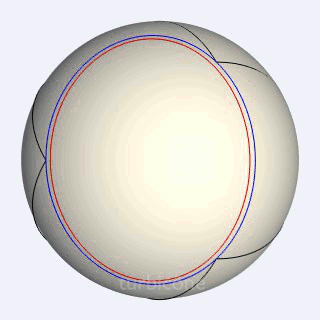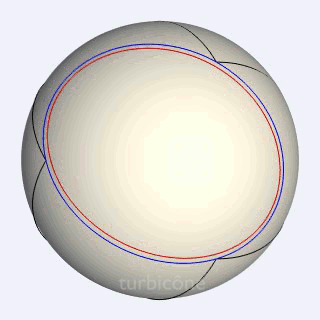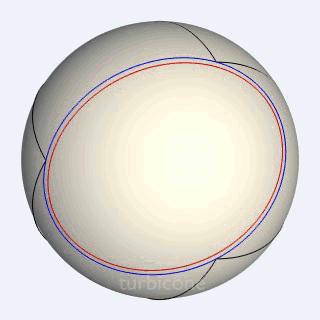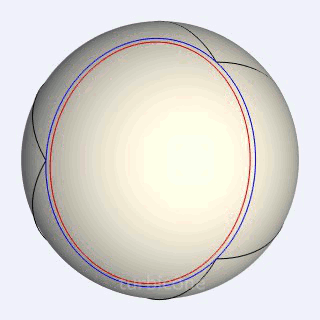
Sans présenter la seconde sphère mentionnée, les Gif ci-dessous montrent l'extrusion conique appliquée au triangle sphérique équilatéral rectangle, et à l'ellipse sphérique du turbicône.

Bien que cette opération paraisse évidente, elle donne des propriétés particulières aux pièces obtenues. L'une en particulier est que les volumes V de ces pièces sont tels que
V = k A
où A est l'aire de la surface délimitée par la courbe sphérique génératrice.

En y regardant de plus prêt, cela signifie que les rapports des volumes générés par l'extrusion conique, sont directement proportionnels aux surfaces des courbes sphériques génératrices. Autrement dit, les rapports volumétriques des machines générées par extrusion conique sont indépendants des rayons des sphères qui les délimitent.

Cela veut dire aussi que pour étudier les rapports volumétriques il suffit d'étudier les rapports des surfaces sphériques impliquées : et c'est pas mal plus simple.

L'extrusion conique est équivalente à l'extrusion cylindrique que l'on peut faire à partir de courbes planes. Les rapports volumétriques observent alors les mêmes règles et il suffit de les étudier à partir des surfaces délimitées par ces courbes, dans le plan.

Le turbicône, la machine FF et les machines ZZ utilisent l'extrusion conique (à l'exception d'une ZZ plano-sphérique définie par Pascal). Plusieurs autres machines sphériques existantes n'utilisent pas cette opération, et sont, de mon point de vue, plus compliquées.

On peut ainsi voir les machines utilisant l'extrusion conique comme des machines 2D : la latitude et la longitude... C'est juste le support de base qui est sphérique au lieu d'être plan...

à plus

Yves

[pascal HA PHAM]

Bonjour tous,

et grand merci à toi Yves pour cet énorme travail de pédagogie autour d'un concept aussi novateur que vaste.
le temps des machines de cinématique 3 D est bel et bien arrivé, petit a petit nous pénétrons dans un nouveau monde.

La cinématique 2D a probablement révélé tous ses registres potentiels en terme de construction de machines pertientes & l' indispensable changement de paradigme se produit maintenant.

Encore fallait il la maîtiser cette cinématique 3D !
Tu nous démontre magistralement que c'est le cas.

La notion d'extrusion conique est tout à fait intéressante, il ne me semble pas encore avoir lu cela dans les bobliographies du web...peut être est ce une première ?

A+

Pascal

[Turbi]

Bonjour Pascal,

Je crois en effet que la sphère n'est pas traitée à sa juste valeur. Son potentiel extraordinaire est quand même bien connu. Depuis longtemps, la principale raison de son absence de la mécanique réside dans la difficulté d'usinage. Ce n'est plus vrai. Aujourd'hui on sais faire. Il suffit de commencer et très vite les techniques vont même s'améliorer car il y a beaucoup de marge de manœuvre.

Comme je l'ai mentionné précédemment, l'extrusion conique utilisée dans nos concepts ramène à une forme simplifiée du 3D : c'est plutôt de la géométrie 2D faite sur une sphère (latitude et longitude). Cette simplification devrait normalement se traduire aussi dans l'usinage.

La géométrie de la sphère est bien connue et on trouve de plus en plus facilement sur le WEB des documents qui en parlent, et pas uniquement Wikipedia. Il suffit d'utiliser Google et de chercher "ellipse sphérique" par exemple pour trouver des tas de choses sur le sujet. Et il y a bien sûr toute la connaissance détenue par les milieux de l'Enseignement...

Bref Pascal, je ne parle que de choses connues. Et je crois que même les GIF que je fais avec Blender et Gimp pourraient être faits avec un logiciel spécialisé (mais pas gratuit).

J'essaye donc surtout de faire mousser la chose à ma manière.

À bientôt

Yves

[Turbi]

Pascal,

C'est bien vrai que 'Extrusion' n'est pas le mot qu'il faut pour ce que je décris. Mais quel mot utiliser ? As-tu une idée ?

Yves