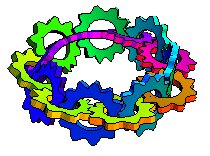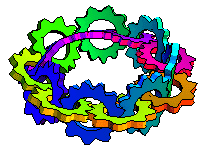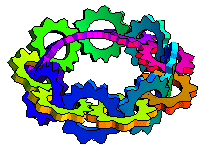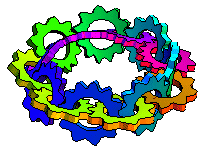Machine Rotative à Piston Annulaire Tri Lobique

[pascal HA PHAM]

bonjour à tous,

GIF GIG GIF HOURRA !



Oui cette nouvelle façon de présenter un mécanisme, une cinématique ou une géométrique évolutive est formidable, et Yves devient un expert/spécialiste en la matière !

Encore BRAVO à lui....

tiens....pour la route : 6 gifs origine wikipedia, Starpsi & mathworld + 1 de Yves :

roue de genève / croix de malte :







mobius trefoil knot :


mobius gear :



pignons :



Wankel :


AU passage notre ZZ 2 c'est en quelque sorte un WANKEL-TRILOBIQUE en 3 D ....!





Super tout cela : de quoi motiver n'importe quel réfractaire aux inventions, aux maths, à la géométrie et à la mécanique !

Pascal

[Turbi]

Coucou,

Quand tu disposes déjà d'une séquence d'images pouvant être assemblées (des jpeg par exempe), c'est vraiment très simple avec Gimp.

1) télécharge Gimp et installe le. C'est gratuit et ca marche du premier coup sans rien d'autre à faire.

2) ouvre la première image de la série avec Gimp

3) les autres images doivent être ouvertes en Calque dans l'ordre de la séquence (il est possible de les ouvrir toutes d'un seul coup)

4) Il suffit d'utiliser ensuite 'Enregistrer Sous'... Il faut alors donner le nom à l'animation, et choisir l'extension 'Gif' (en bas de la fenêtre)

5) Une fenetre arrive alors dans laquelle il faut sélectionner 'Animation' (la seconde option)

6) Une nouvelle fenetre permet de préciser le délai entre deux images consécutives.

7) Dès que le gif est fait il faut l'essayer en l'ouvrant directement dans IE ou dans Frefox.

Ca peut sembler compliqué... Mais c'est vraiment très simple!!!!

Essaye et dis-moi ce que tu en penses
Yves

[pascal HA PHAM]

message bien reçu !
j'essaierais dès que possible !
A+

[pascal HA PHAM]

bonjours à tous,

Ca y est Yves m'a donné tout ce qu'il fallait pour devenir progressivement autonome dans la confection d'animation GIF
- le logiciel libre "GIMP"
- la méthode d'utilisation
- ses astuces et sutout son expérience de pionnier.

Voilà ce que cela donne :

ETAPE CONCEPTION :
3 early trilobiques avec pour origine des fichiers Excel "pixélisés" et colorés /animés en planches succéssives via des programmations / fonctions Visual basic que j'ai adaptées aux différentes cinématiques.

ETAPE TRANSPOSITION :
formater, indexer et caler les feuilles EXCEL en version image BMP
avec respect des tailles d'images et surtout de l'indexation (en positionnement orthonormé dans chaque feuille) et surtout en organisation de séquence.

puis ETAPE MISE EN GIF par GIMP.

envoi de Yves :


mes deux essais d'hier soir.






Les initiés retrouveronts les mouvements génériques datants de 2002 et 2003 & qui me sont si chers.....

D'ici peu il y en aura d'autres : la pompe à gif est désormais amorcée....et de belle façon

N.B. : il y a entre 8 et 10 calques par gif et le poids de chaque fichier d'animation ne dépasse pas 70 ko.



A+

Pascal

[pascal HA PHAM]

bonjour,

Et les mathématiques dans tout cela ?

petit gif qui illustre des fonctions génériques F(x ) permettant de retrouver le nombre "e" (base des log Népériens) :



trace bleu :
F(x) = (1+1/x)^x qui tend vers "e" par valeur inférieure quand x tend vers l'infini.
nota : x appartient à l'ensemble des entiers naturels.

trace rouge :
F(x) = ((1+1/x) / (1-1/x))^(x/2) qui tend vers "e" par valeur supérieure quand x tend vers l'infini.

Trace verte :
perfectionnement de la deuxième avec apparition de la sous fonction f'(x) en lieu et place de x :

F(x) = ((1+1/2*f'(x)) / (1-1/2*f'(x))))^(f'(x))....

Cette 'best fonction' tend vers "e" quand x tend vers l'infini avec une rapidité dépendant de f'(x).et qui peut être étonnante quand f'(x) est du style f'(x) = (x)^x...ou mieux ((x)^x)^x....ou encore mieux ((((x)^x)^x))^x par exemple avec f'(x) = (x)^x une précision à la neuvième décimale de "e" est atteinte pour x= 7 ! et on peut faire bien plus rapide en jouant avec f'(x)...pour peu que l'on possède un ordinateur performant !

la best fonction qui résume "e" par le calcul affiche son "extension cinématique" dans les 3 dimensions" (x, y et f'(x))

BIBLIOGRAPHIE :

avec f'(x) = x^x la 'best fonction' donne 2,7182818282595900 au rang x = 7

nb « e » par wikipédia :

http://fr.wikipedia.org/wiki/E_(nombre)
il est dit :
« l'expression décimale commence par 2,718 281 828 459 045 235 360 287 4… »

NOTA : la fonction "trace bleu" du gif est mentionnée comme étant connue depuis longtemps (Bernouilli ?)…
Mais les "trace rouge" et "trace verte" avec leur tendance beaucoup plus rapide par valeur supérieure ne semblent pas l’être.


Avis aux amateurs !


les mathématiques ? c'est super beau...et ça développe l'esprit.

Autres gifs réalisés dernièrement :
ils concernent la cinématique générique du TRILO :

A partir du triangle de notre ami Franz Reuleaux :



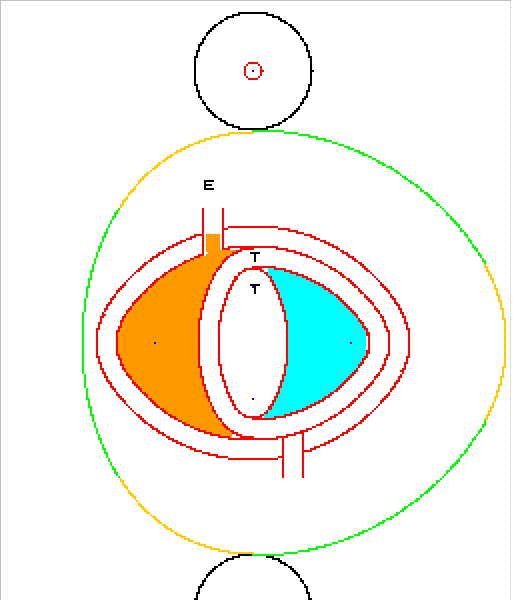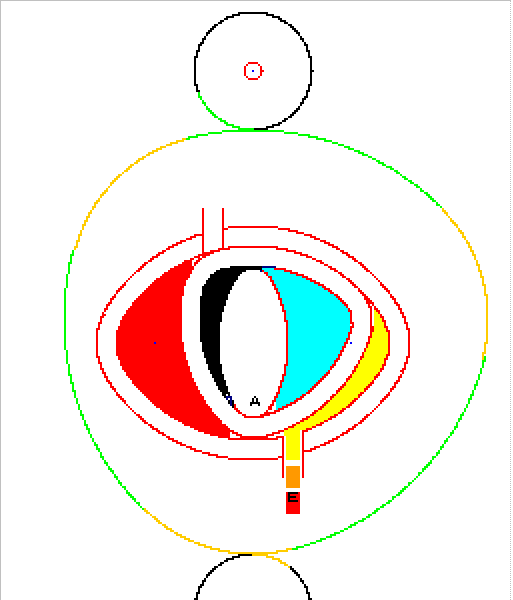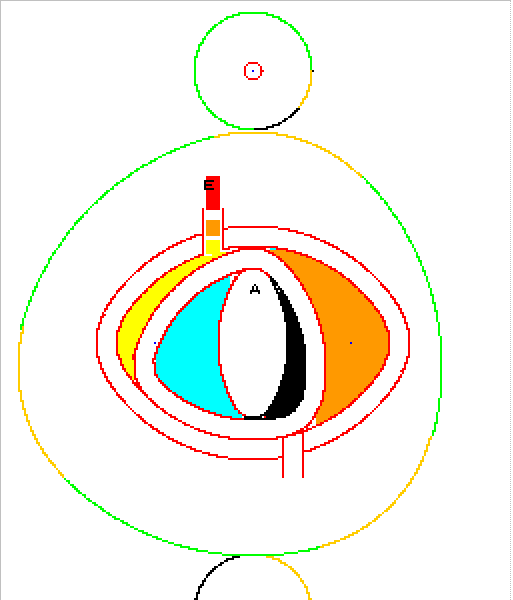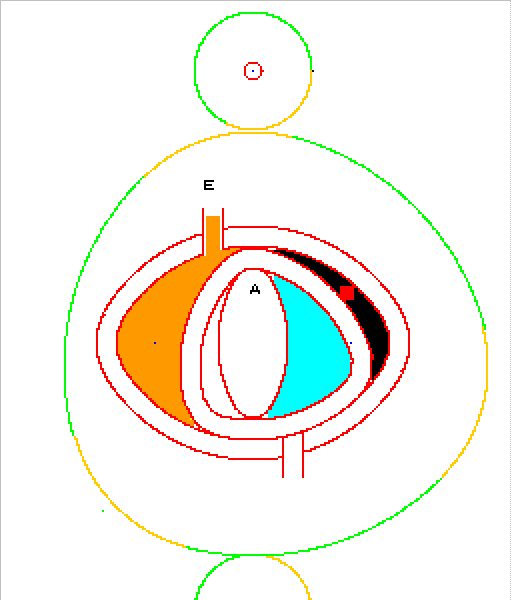
Mais la rotation n'est pas dans le bon sens :
Amélioriation :







avec le code visual basic permettant de pixeliser une feuille Excel normale (avec attribution d'un fond jaune) :
......

Sub formatpixel()
Application.ScreenUpdating = False
Cells.Select
Selection.RowHeight = 2
Selection.ColumnWidth = 0.2
Selection.Interior.ColorIndex = 6
Range("x25").Select
End Sub

.......

Et le code permettant de génerer les différentes silhouettes paramètres de la famille TRILOBIQUE :

......

Sub varitrilob()
Application.DisplayFullScreen = True
Application.OnKey _
Key:="{F1}", procedure:="varitrilob"
Application.OnKey _
Key:="{F2}", procedure:="formatpixel"
Application.Run "pixelmacro21.xls!formatpixel"
For nbfois = 1 To 4
n = nbfois
'valeur de la séquence en °
seq = 30
'
K = 0.0043633
'cal est le paramètre de décalage angulaire de positionnement du segment d'aile
'du piston annulaire tri lobique selon l'ampleur du noyau
'environ 33 de cal par trancche de 0,25 de coef
'
'grosse basse
If n = 4 Then
col = 39
Range("a1").Offset(290, 160).Select
coef = 0.25
cal = -41
End If

'bosse
If n = 3 Then
col = 4
Range("a1").Offset(200, 50).Select
coef = 0.5
cal = -8
End If
'normal
If n = 2 Then
col = 3
Range("a1").Offset(140, 160).Select
coef = 1
cal = 58
End If
'creux
If n = 1 Then
col = 8
Range("a1").Offset(60, 35).Select
coef = 1.25
cal = 91
End If
'rayon de base théorique
rbt = 60 / coef
'
PRG = rbt * 9 / 10 'PR : distance Générique entre les centres de rotation
R = Fix(PRG * coef) 'R : rayon de la chambre trilobique
RG = PRG * coef 'Rg : rayon générique de la chambre trilobique
PR = Fix(RG * coef) 'PR : distance entre les centres de rotation
rn = Fix(PRG * coef * 0.98 ) 'rn =rayon extérieur pîston ftri lobique
ep = Fix(PRG * coef * 0.98 * 0.25) 'ep : épaisseur du noyau
rb = Fix((RG - PRG) * 1.04 / Cos(K * cal / 5)) 'rb : rayon des 2 bosses latérales
'
ActiveWorkbook.Names.Add Name:="dep1", RefersToR1C1:=ActiveCell
ActiveWorkbook.Names.Add Name:="dep2", RefersToR1C1:=Range("dep1").Offset(0, PR)
ActiveWorkbook.Names.Add Name:="dep3", RefersToR1C1:=Range("dep1").Offset(-Fix(PR * Sin(240 * K)), Fix(PR * Cos(240 * K)))
Range("dep1").Interior.ColorIndex = 1
Range("dep2").Interior.ColorIndex = 1
'
If nbfois = 1 Then
'traçage lobe
Range("dep1").Select
For i = 900 + cal To 1150 + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 60 - cal To 300 - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
Range("dep2").Select
For i = 420 + cal To 670 + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 1020 - cal To 1260 - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
Range("dep3").Select
For i = 1380 + cal To 1630 + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 540 - cal To 780 - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
'End If
Application.ScreenUpdating = True
'End If
'premier détraçage en blanc
Application.ScreenUpdating = False
Range("dep1").Select
For i = 900 + cal To 1150 + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 60 - cal To 300 - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
Range("dep2").Select
For i = 420 + cal To 670 + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 1020 - cal To 1260 - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
Range("dep3").Select
For i = 1380 + cal To 1630 + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 540 - cal To 780 - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
End If
Application.ScreenUpdating = False
'rotation de 60° autour du centre dep 1
For dec = 0 To 240 Step seq
'traçage lobe en noir hexa-arc en vert
Application.ScreenUpdating = False
ActiveWorkbook.Names.Add Name:="dep2", RefersToR1C1:=Range("dep1").Offset(Fix(PR * Sin(dec * K)), Fix(PR * Cos(dec * K)))
ActiveWorkbook.Names.Add Name:="dep3", RefersToR1C1:=Range("dep1").Offset(-Fix(PR * Sin((240 - dec) * K)), Fix(PR * Cos((240 - dec) * K)))
Range("dep1").Select
'lobe
For i = 900 + dec + cal To 1150 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 60 + dec - cal To 300 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
'
'lobe
Range("dep2").Select
For i = 420 + dec + cal To 670 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 1020 + dec - cal To 1260 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
'lobe
Range("dep3").Select
For i = 1380 + dec + cal To 1630 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 540 + dec - cal To 780 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
Application.ScreenUpdating = True
'détraçage en blanc
Application.ScreenUpdating = False
Range("dep1").Select
'lobe
For i = 900 + dec + cal To 1150 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 60 + dec - cal To 300 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
'lobe
Range("dep2").Select
For i = 420 + dec + cal To 670 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 1020 + dec - cal To 1260 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
'lobe
Range("dep3").Select
For i = 1380 + dec + cal To 1630 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 540 + dec - cal To 780 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
Application.ScreenUpdating = True
Next
'rotation de 60° autour du centre initial dep 2 (rebaptisé dep1)
ActiveWorkbook.Names.Add Name:="mémo", RefersToR1C1:=Range("dep3")
ActiveWorkbook.Names.Add Name:="dep1", RefersToR1C1:=Range("mémo")
ActiveWorkbook.Names.Add Name:="dep2", RefersToR1C1:=Range("dep1")
ActiveWorkbook.Names.Add Name:="dep3", RefersToR1C1:=Range("dep2")
For dec = (720 + seq) To 960 Step seq
'traçage lobe en noir et hexa-arc en vert
Application.ScreenUpdating = False
ActiveWorkbook.Names.Add Name:="dep2", RefersToR1C1:=Range("dep1").Offset(Fix(PR * Sin(dec * K)), Fix(PR * Cos(dec * K)))
ActiveWorkbook.Names.Add Name:="dep3", RefersToR1C1:=Range("dep1").Offset(-Fix(PR * Sin((240 - dec) * K)), Fix(PR * Cos((240 - dec) * K)))
Range("dep1").Select
'lobe
For i = 900 + dec + cal To 1150 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 60 + dec - cal To 300 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
'lobe
Range("dep2").Select
For i = 420 + dec + cal To 670 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 1020 + dec - cal To 1260 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
'lobe
Range("dep3").Select
For i = 1380 + dec + cal To 1630 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
For i = 540 + dec - cal To 780 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = 1
Next
Application.ScreenUpdating = True
'détraçage en blanc
Application.ScreenUpdating = False
If dec < 960 Then
Range("dep1").Select
'lobe
For i = 900 + dec + cal To 1150 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 60 + dec - cal To 300 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
'lobe
Range("dep2").Select
For i = 420 + dec + cal To 670 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 1020 + dec - cal To 1260 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
'lobe
Range("dep3").Select
For i = 1380 + dec + cal To 1630 + dec + cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
For i = 540 + dec - cal To 780 + dec - cal
x = Fix(Sin(K * i) * R)
Y = Fix(Cos(K * i) * R)
ActiveCell.Offset(x, Y).Interior.ColorIndex = col
Next
End If
Application.ScreenUpdating = True
Next
Next
'Next
Range("x25").Select
Range("dep1").Interior.ColorIndex = 1
Range("dep2").Interior.ColorIndex = 1
End Sub

.........

Ce code permet d'obtenir le traçage automatique et dynamique de ces 4 paramètrages différents du TRILOBIQUE (et en partant d'une feuille EXCEL tout à fait normale) :






A+

Pascal

[Remundo]

Salut Pascal,

tout ça me rappelle certains des gif que j'avais faits il y a longtemps...

Mais il y en a de nouveaux, très réussis...

Si vous cherchez une fonction hyperdivergente...

Essayer x! (x factorielle)

Et si ça ne suffit pas... x! ^ x ! ^x! .... ^x!

Il y avait aussi la fonction gamma d'Euler qui généralise la factorielle à des nombres non entiers réels positifs...

Oh là, ce sont de vieux souvenirs de maths sup / Maths Spé...

à+

[pascal HA PHAM]

Oui Raymond ! & maintenant le Team maîtrise plutôt bien les gifs !

sinon en maths, par exemple, il y a aussi :

Autre biblio sur « e »

http://serge.mehl.free.fr/anx/calcul_elem_e.html

+ sur la trigo sphèrique chère à nos chères inventions (ZZ) :

http://fr.wikipedia.org/wiki/Trigonom%C ... C3%A9rique

A+






Pascal

[pascal HA PHAM]

bonjour tout le monde,

« Certains disent
Que les triangles
Parlent aux sphères
Et que des ellipses s'en mêlent

Certains les pousseraient même
A faire des mouvements
Peu recommandables

Mais tout cela n'est que le bruit des imaginations

Il ne faut pas écouter
Ces courants révolutionnaires

Mais seulement regarder leur orchestration,
Et savourer pleinement la chose »


Hé Franz, si tu as le temps,
regarde en bas : en synthèse, qu'en penses tu ?







Yves est à l'orchestration.

TRIANGLE SPHERIQUE & SA CINEMATIQUE 3D





commentaires de Yves SAUGET :
« Mais là aussi il faut faire attention : la petite ellipse du centre n'en est pas vraiment une. Cette courbe en est très proche à tel point que si je dessinais une ellipses avec les mêmes axes, les deux paraîtraient confondues. Pourtant, les formules montrent hors de tout doute qu'il y a cette infime différence.

Il est également possible de regarder la courbe que fait le centre de l'ellipse sur le triangle...

À plus »


A+ aussi

Pascal

[pascal HA PHAM]

bonjour,



VOUS POUVEZ ENFIN ENTENDRE RUGIR LE MOTEUR TURBINE "cliquez" :

http://www.ipernity.com/doc/pascalhapham/8556708/

Voilà les amis :
"une oeuvre ....une vie"

les premiers tomes de 4 vidéos sur le moteur "Turbine Thermique Volumètrique de Jean Claude LEFEUVRE".


Grace à la diligence de Raymond qui à réalisé de beaux montages en reprenant les vidéos originales / d'époque de Jean Claude.

Je ne pensais pas qu'un tel exploit technologique pouvait être réalisé par un humain : de l'abnégation à l'état pur...un résulat exemplaire et tout à fait incroyable.

Merci Jean tu montres à la terre entière ou sont les vraies valeurs de la vie : l'intelligence, la passion, le courage, le travail et la détermination.

A+



Pascal

[pascal HA PHAM]

bonjour,

la suite = vidéos TOME 2 et 3 :

http://www.ipernity.com/doc/pascalhapham

A+

Hé Jean Claude attend nous !

Pascal