Cuicui a écrit :bigeasy a écrit :pour piloter les palettes dans la turbine rotative en remplacement de la came centrale il suffit d'aller dans la boite du "MECANO"
utiliser le système tel que le dessin les secteurs-piston sont remplacés par des bras dont les extrémités sont fixés au centre de chaque bielle du lozange
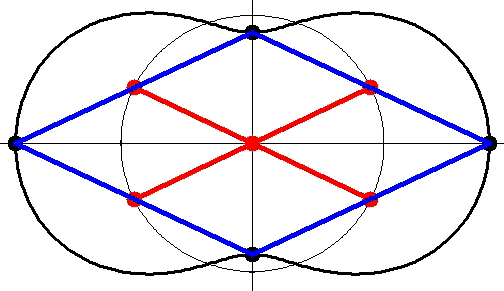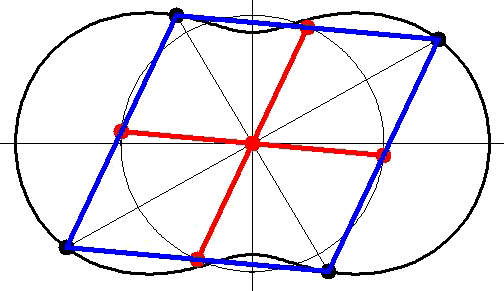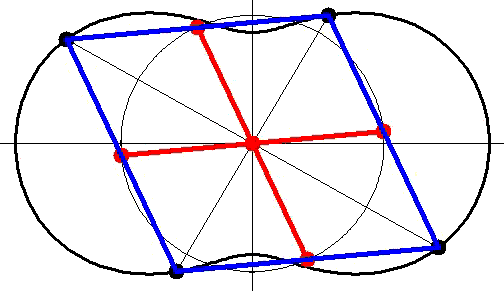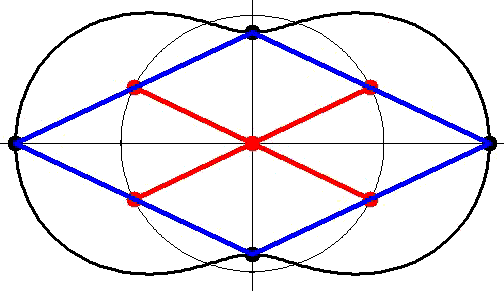
Elégant !
Bonjour,
Oui, tout à fait pour la boite de mécano : et ceci a été consigné dans le magnifique brevet N° FR 80 23 551 (dépôt du 03 11 1980)de Jean Pierre AMBERT ...c'est bien de le signaler ici, merci Bigeasy et Cuicui, j'ai par devers moi les études complètes de la géomètrie du MRDL réalisées par Jean Pierre à l'époque mais je ne puis les publier sans son accord implicite.
Avec mon ami Yves SAUGET nous avions planché sur la fameuse version 3 palettes sans savoir que Jean Pierre l'avait découverte avant nous, qu'importe cela n'empêche pas Yves de retravailler dessus et d'y apporter de la plus value supplémentaire :
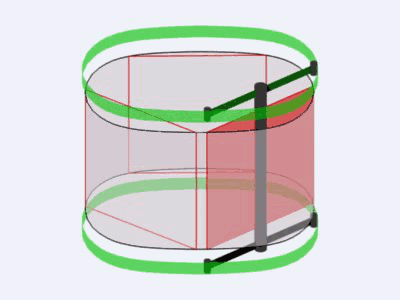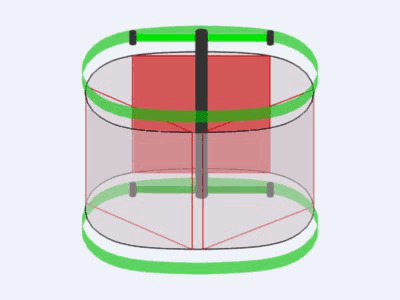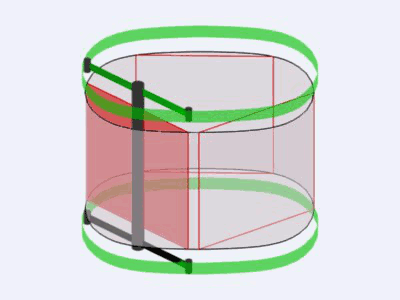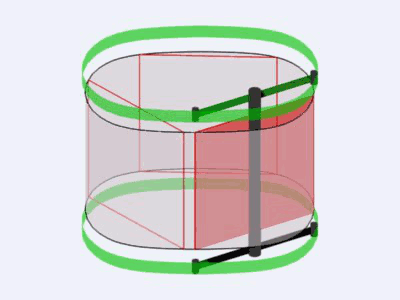

voir le fil de discussion de Yves sur son "TURBICONE" et ces machines
https://www.econologie.com/forums/post195347.html#195347
SYNTHESE
Ce que j'ai cherché à faire avec mon concept à bielle BIPP RVCC ?, c'est avant tout proposer un concept qui puisse piloter de 1 à n palettes sans pour autant utiliser une double came centrale comme l'a montré bigeasy dans le joli éclaté plus haut.
En corrolaire, dans ce concept BIPP RVCC, plus il y a de palettes, plus mon villebrequin devra être long pour intégrer la largeur des 2 bielettes requises par palettes....le calcul mini du nb de palette est (2*n)-1 car la première des n palettes ne pourra comporter qu'une seule bielette, exactement placée dans l'axe mediant.
Ce concept est en permier dédié à une mise en ouevre non thermique.
Sauf utilisation d'une double came centrale, aucun concept de pilotage de palettes n'offre un contrôle parfait des amplitudes de palettes pour n différent de 4....maintenant c'est chose faite.
J'attend la publication du concept imaginé par Raymond en octobre 2010 : il semble qu'il ai trouvé une autre solution de pilotage rigoureux par pignons...
QUESTION :
"Raymond, est ce valable pour n palettes ou pour un nb figé à 4 ?....on est impatient de savoir !"
Je vous remet ici une synthèse d'ensemble des dessins principaux et animations du BIPP RVCC bout à bout (avec abrégé du brevet) :
ABREGE
L’invention est une machine de type turbine volumétrique permettant de convertir en énergie mécanique des flux naturels éoliens ou hydrauliques, elle accepte aussi une alimentation vapeur vive. Des aménagements permettent de l’utiliser en pompe, en compresseur, ou encore en moteur à combustion interne. Cette machine est intitulée « Turbine volumétrique à palettes pilotées par bielles centrifuges de liaison, munie d’un vilebrequin et d’un rotor support, lesquels sont coaxiaux et tournent en sens inverse », elle exploite les variations de volume crées par des palettes qui tournent et glissent via un rotor, au sein d’un stator de chambre de profil intérieur spécifique, suite à un pilotage réalisé par des bielles. La transmission du mouvement contre rotatif entre le vilebrequin et le rotor est assuré par trois engrenages coniques : un premier est solidaire du vilebrequin, un deuxième solidaire du rotor, le troisième assure la liaison contre rotative entre les deux premiers.
Figure pour l’abrégé : FIG.1


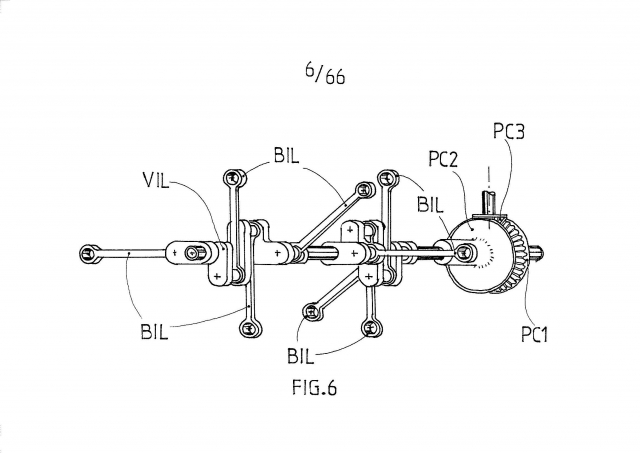
animations :


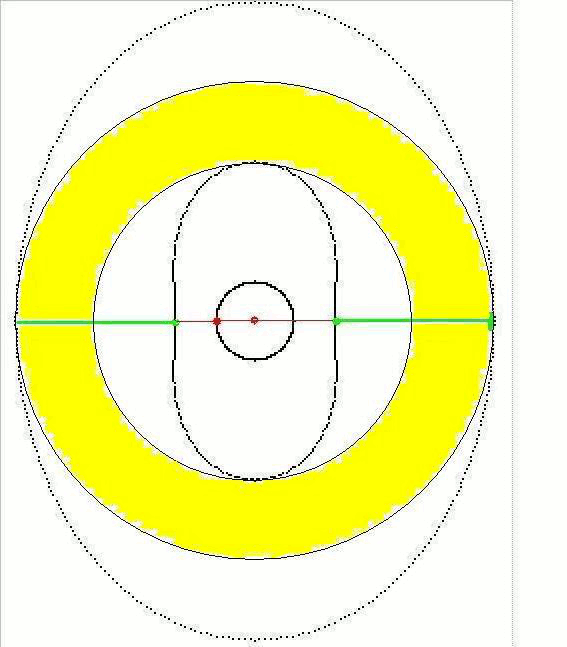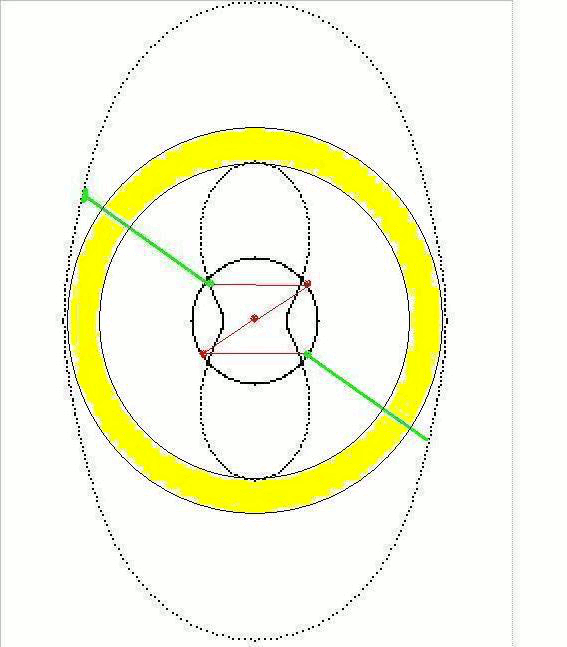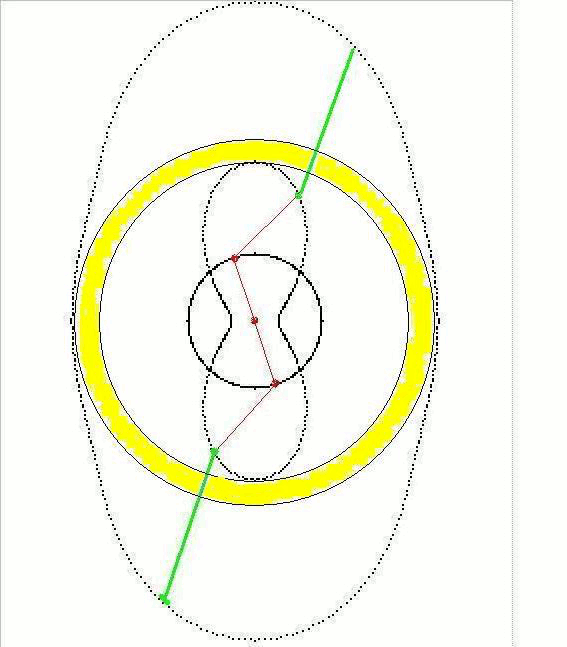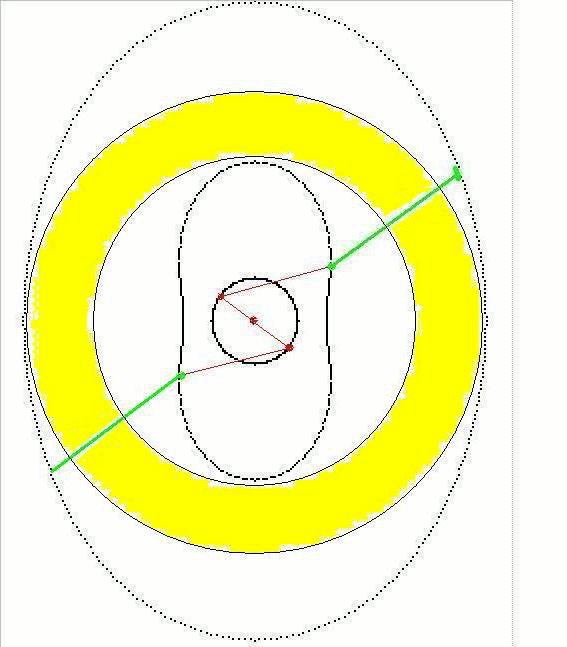
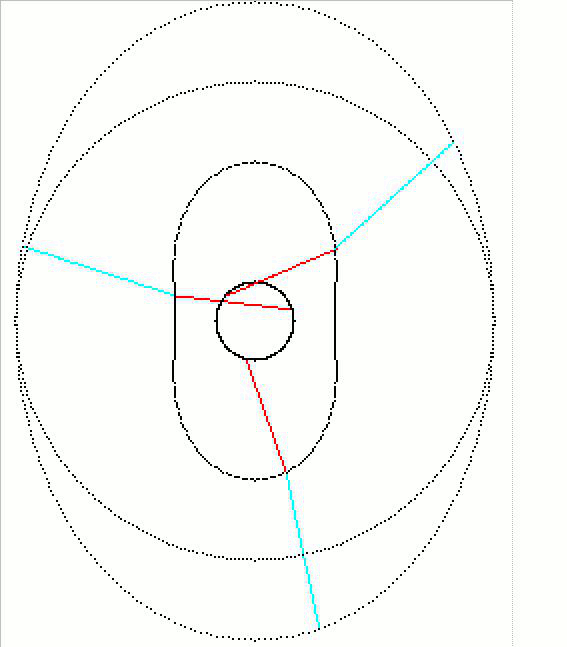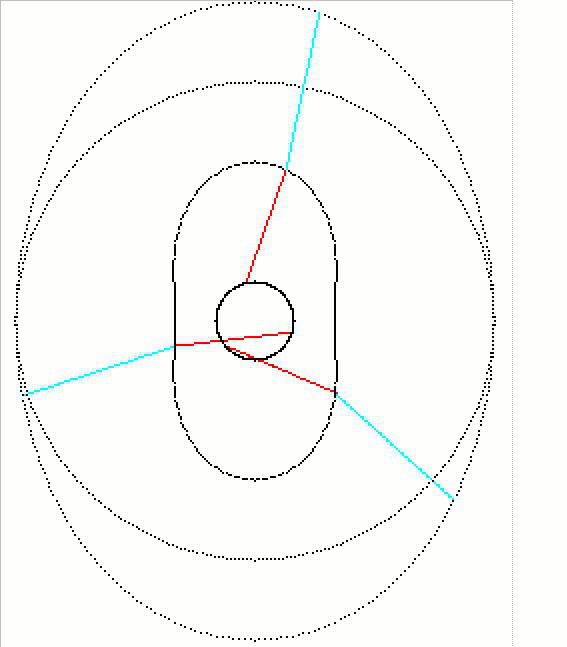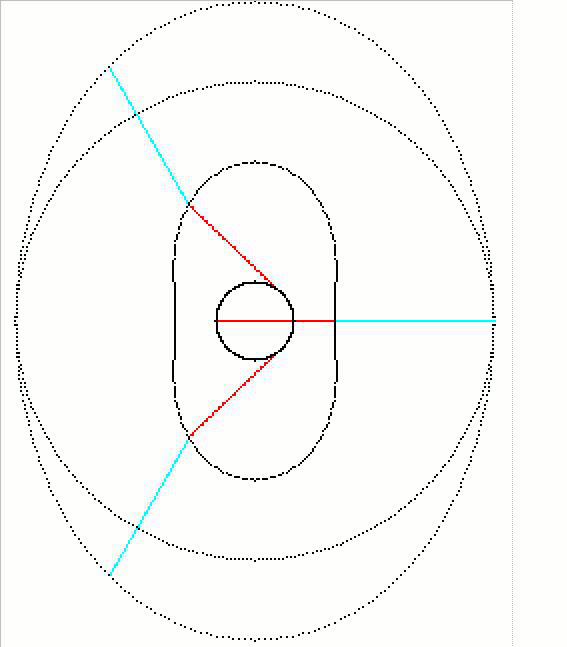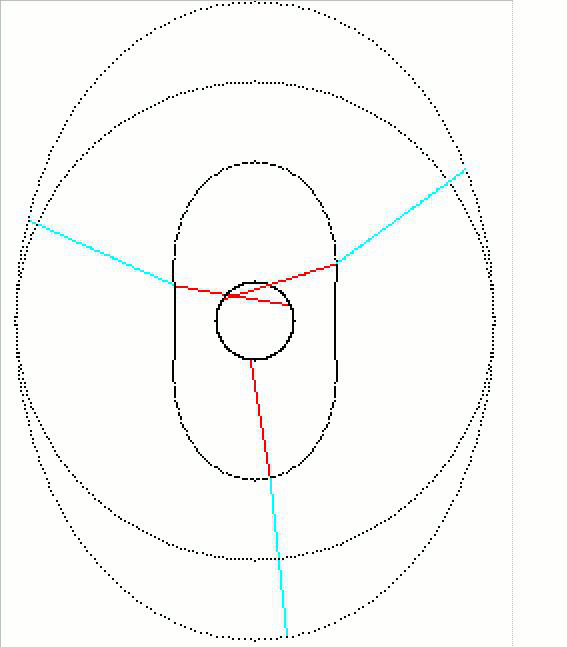

sans oublier les courbes de l'équation polaire qui vont avec :

la génèse "matheuse" du concept BIPP RVCC :
GEOMETRIE DESCRIPTIVE ET ANALYTIQUE A LA BASE DE L’INVENTION
Base descriptive conceptuelle du mouvement générique figure N° 2 :
Une ligne brisée composée de 3 segments de longueurs fixes OA, AB, et BP est organisé et évolue autour d’un point de rotation O de la façon suivante :
- le premier segment OA tourne autour du point O
- le deuxième segment AB est articulé au premier segment en son extrémité A et son extrémité B tourne autour du point O, selon la même vitesse angulaire, mais en sens inverse en respectant un glissement radial suivant l’axe de la demi-droite de direction OB
- le troisième segment BP est articulé au deuxième segment en son extrémité B et son extrémité P tourne en respectant un alignement continu et parfait des trois points O, B et P.
La figure N° 2 montre deux positions angulaires des deux premiers segments de la ligne brisée ainsi décrite. L’ensemble des triangles représentés permet, par démonstration, d’établir une équation polaire afférente à la courbe d’évolution du point B dont la distance à O varie continuellement dans un intervalle de longueurs allant de (AB – OA) à (AB + OA)
Une nouvelle équation polaire caractérise l’ensemble des points de la courbe de révolution du point B, l’équation s’écrit : (AB) 2 = sin2(θ)*(OB-OA)2 + cos2(θ)*(OB+OA)2
Nota : (OA) et (AB) sont les paramètres fixes de cette équation polaire, laquelle peut aussi se traduite en une fonction de variable du type OB = f (θ), le segment BP n’est pas représenté sur la figure N° 2 afin de ne pas compliquer les dessins.
DEMONSTRATION, OBTENTION DE L’EQUATION POLAIRE
La figure N° 2 est encore en référence. : h = (OB + OD)* cos (θ),
v = (OB + OD)* sin (θ) – AD ; or OD = OA et AD = 2*OA (sin (θ)
donc : v = sin (θ) * (OB – OA)
considérons maintenant le triangle (A B C) :
(AB) 2 = ( AC) 2 + (BC) 2 avec h = (BC) et v = (AC)
on remplace alors AC et BC par les valeurs respectives de v et de h calculées plus haut:
(AB) 2 = (sin (θ) * (OB –OA)) 2 + ((OB + OD)* cos (θ)) 2; or OD = OA
au final: (AB) 2 = sin2(θ)*(OB-OA)2 + cos2(θ)*(OB+OA)2
Affectation des données théoriques de l’équation aux éléments physiques de la machine :
(AB) = longueur entre les deux articulations d’une bielle, (OB) = longueur polaire variable entre le centre O et la courbe polaire de révolution qui est imposée à l’articulation B (entre bielle
et palette), au cours d’une révolution complète, (OA) = rayon de révolution du (des) maneton de vilebrequin
son dessin "de démo" :

un double clin d'oeuil :
existe déja avec un bi cylindre normal :


comme le dit Orbes plus haut : "et pourtant elle (s) tourne"
A+
Pascal