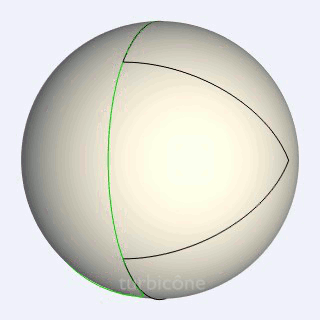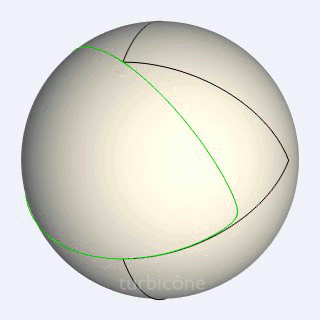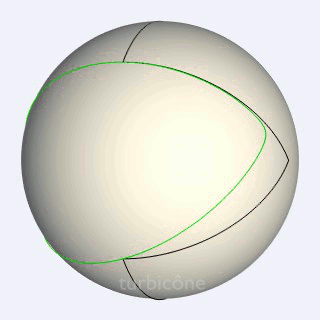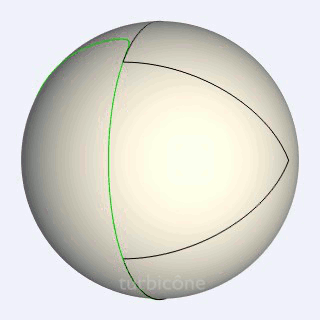
Voici une autre façon de voir la géométrie du turbicône

Cette fois les ellipses sphériques sont fixes. C'est le triangle sphérique qui tourne.
À +
Yves







Attention, sur ce dessin,seules les courbes rouges sont elliptiques, les blanches ne sont que des parallèles aux rouges. Une particularité tout de même : les deux rouges sont aussi parallèles entr'elles. Autrement dit, "une ellipse sphérique est parallèle à sa complémentaire".pascal HA PHAM a écrit :en son temps yves avais aussi réalisé cette belle cartographie du registre des cônes élliptiques :
pascal HA PHAM a écrit :mais j'ai un peu de mal à immaginer ce qui se passe au milieu sur ton concept :
...
dis yves : pourrais tu nous tracer/ajouter la cinématique du centre de gavité de ce triangle sphèrique qui glisse parfaitement entre ses deux profils en cônes elliptiques ?

















Revenir vers « Sciences et technologies »
Utilisateurs parcourant ce forum : Aucun utilisateur inscrit et 92 invités