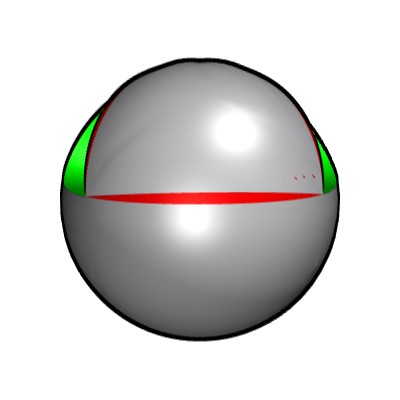
Voici donc une première image qui montre en vert le cône complémentaire du turbicône. La sphère centrale est là pour aider à la visualisation des formes. Si les objets présentés ressemblent maintenant à des pièces solides plus qu'à des concepts de géométrie, ce n'est que pour aider à la compréhension des formes. Les machines viendront plus tard.
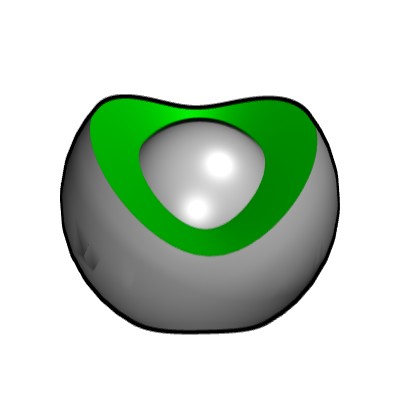
On peut facilement imaginer la sphère qui ferme l'espace du cône.
La déformation située au bas de la sphère correspond au bord de la partie symétrique du cône.

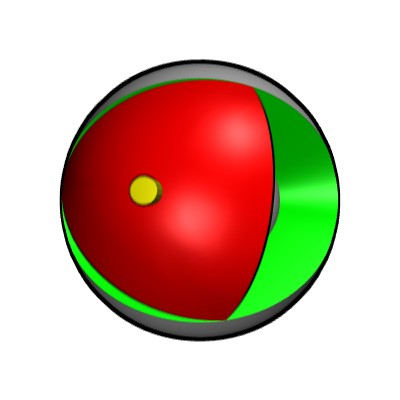
Le trièdre est en place. Une partie sphérique (non présentée) lui a été retirée de façon à ce qu'il glisse sur la sphère centrale.

Le trièdre à tourné (donc glissé sur la sphère centrale). On voit maintenant une de ses faces en rouge.
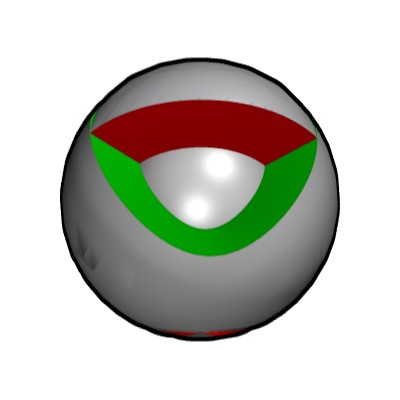
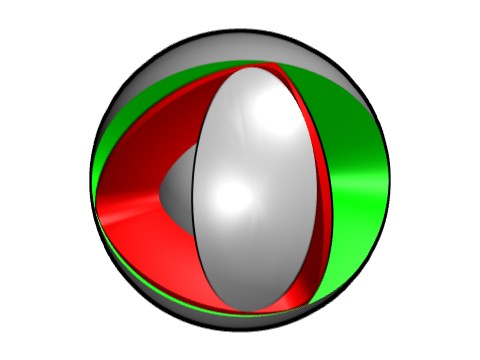
Un nouveau déplacement du trièdre permet à l'espace au premier plan d'atteindre son volume maximum.
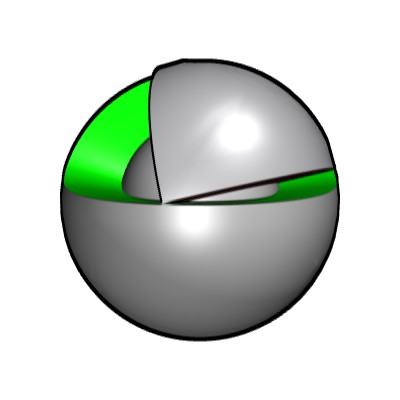
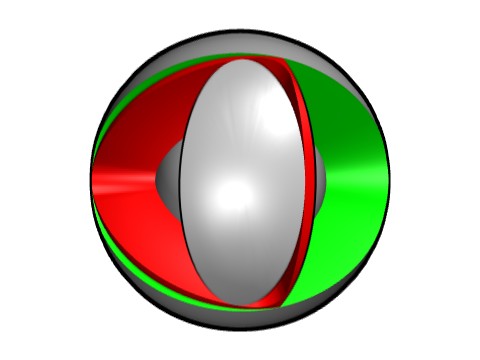
Vue d'un autre angle.

L'espace au premier plan a atteint son minimum. La variation volumétrique est considérable.
La suite pour bientôt
Yves